集成算法
1.集成学习的概念
集成学习(ensemble learning)从概念上讲,它并不是一个单独的机器学习算法,而是通过构建并结合多个机器学习器来完成学习任务。也就是我们常说的“博采众长”。集成学习可以用于分类问题集成,回归问题集成,特征选取集成,异常点检测集成等等,可以说所有的机器学习领域都可以看到集成学习的身影。
我们可以对集成学习的思想做一个概括。对于训练集数据,我们通过训练若干个个体学习器,通过一定的结合策略,就可以最终形成一个强学习器,以达到博采众长的目的。
集成算法一般分为三类:Bagging,Boosting,Stacking(我们可以把它简单地看成并行,串行和树型)。

2.bagging算法思想
bagging是bootstrap aggregating的缩写。该算法的思想是让学习算法训练多轮,每轮的训练集由从初始的训练集中随机取出的n个训练样本组成,某个初始训练样本在某轮训练集中可以出现多次或根本不出现(即所谓的有放回抽样),训练之后可得到一个预测函数序列h_1,⋯ ⋯h_n ,最终的预测函数H对分类问题采用投票方式,对回归问题采用简单平均方法对新示例进行判别。上面的算法思想可通过下图来进行理解:
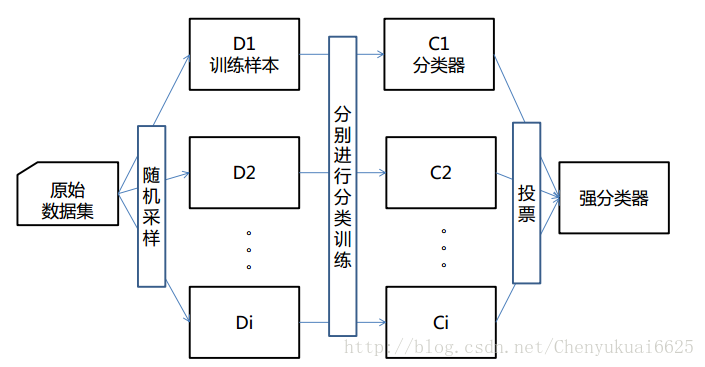
算法的基本流程为:
输入为样本集D={(x,y1),(x2,y2),…(xm,ym)}D={(x,y1),(x2,y2),…(xm,ym)},弱学习器算法, 弱分类器迭代次数T。 输出为最终的强分类器f(x)f(x) (1)对于t=1,2…,T:(a)对训练集进行第t次随机采样,共采集m次,得到包含m个样本的采样集Dm;(b)用采样集DmDm训练第m个弱学习器Gm(x); (2) 如果是分类算法预测,则T个弱学习器投出最多票数的类别或者类别之一为最终类别。如果是回归算法,T个弱学习器得到的回归结果进行算术平均得到的值为最终的模型输出。





3.boosting算法思想
Adaboosting算法是Adaptive boosting的缩写,是一种迭代算法。每轮迭代中会在训练集上产生一个新的分类器,然后使用该分类器对所有样本进行分类,以评估每个样本的重要性(informative)。
具体来说,算法会为每个训练样本赋予一个权值。每次用训练完的新分类器标注各个样本,若某个样本点已被分类正确,则将其权值降低,并以该权重进行下一次数据的抽样(抽中的概率减小);若样本点未被正确分类,则提高其权值,并以该权重进行下一次数据的抽样(抽中的概率增大)。权值越高的样本在下一次训练中所占的比重越大,也就是说越难区分的样本在训练过程中会变得越来越重要。 整个迭代过程直到错误率足够小或达到一定次数才停止。boosting算法在迭代的过程中不断加强识别错误样本的学习比重,从而实现最终的强化学习。


基本思想:先去生成一个分类器,学习出结果C1,看C1训练结果的好坏,第二个分类器重点学习第一个分类器学习错误的样本;
小例子:
分类器非常简单,要么竖着分,要么横着分;

第一次:这样分,结果分错了上面的三个,重点学习上面的三个样本;

第二步:因为给了上面三个样本更大的权重,所以这样分了,左面两个又分错了;

第三步:这样分了

第四步:最后把这三个分类器合起来,就成了这样一个决策边界。
4.Stacking
Stacking训练一个模型用于组合(combine)其他各个基模型。具体方法是把数据分成两部分,用其中一部分训练几个基模型A1,A2,A3,用另一部分数据测试这几个基模型,把A1,A2,A3的输出作为输入,训练组合模型B。注意,它不是把模型的结果组织起来,而把模型组织起来。理论上,Stacking可以组织任何模型,实际中常使用单层logistic回归作为模型。Sklearn中也实现了stacking模型:StackingClassifier 
核心思想:分为两层,第一层主要是多个分类器进行分类输出;第二层主要是学习第一层输出的权重,把第一层的输出作为第二层的输入。